1. 梯度

课程计划

Lecture 4： 手推梯度和算法

  1. 介绍
  2. 矩阵计算
  3. 反向传播

image-20210205231516555

image-20210205231832287

  • 如果给定的函数有一个输出和n个输入
  • 梯度是相对于每个输入的偏导向量

Jacobian Matrix: Generalization of the Gradient

image-20210205233107266

  • 给定一个m个输出和n个输入的函数
  • 其Jacobian是偏导的$m \times n $矩阵

Chain rule

image-20210206194520526

Example Jacobian: Elementwise activation Function

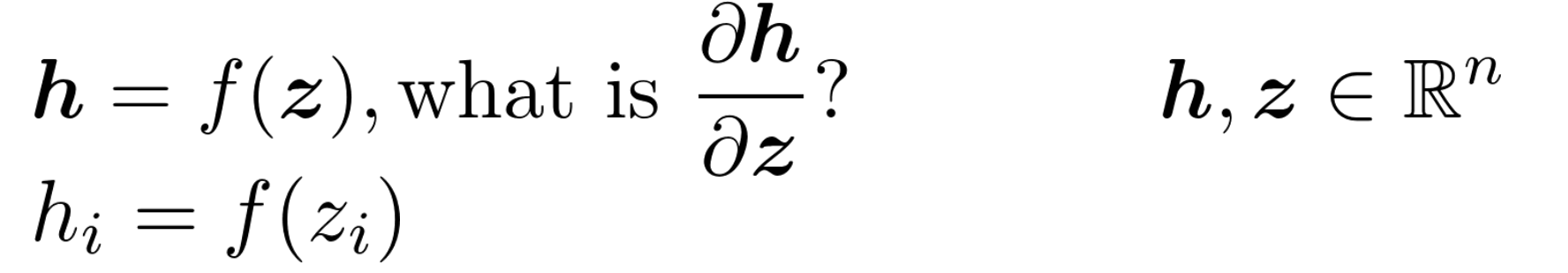
image-20210206194651388

因为n个输入n个输出，其Jacobian矩阵应该是$n \times n$

image-20210206194820897

下面是一些公式，利用定义逐个元素求导很容易证明。

image-20210206200713639

image-20210206200750535

2. Back to our Neural Net!

模型如下，一个隐层的简单架构。

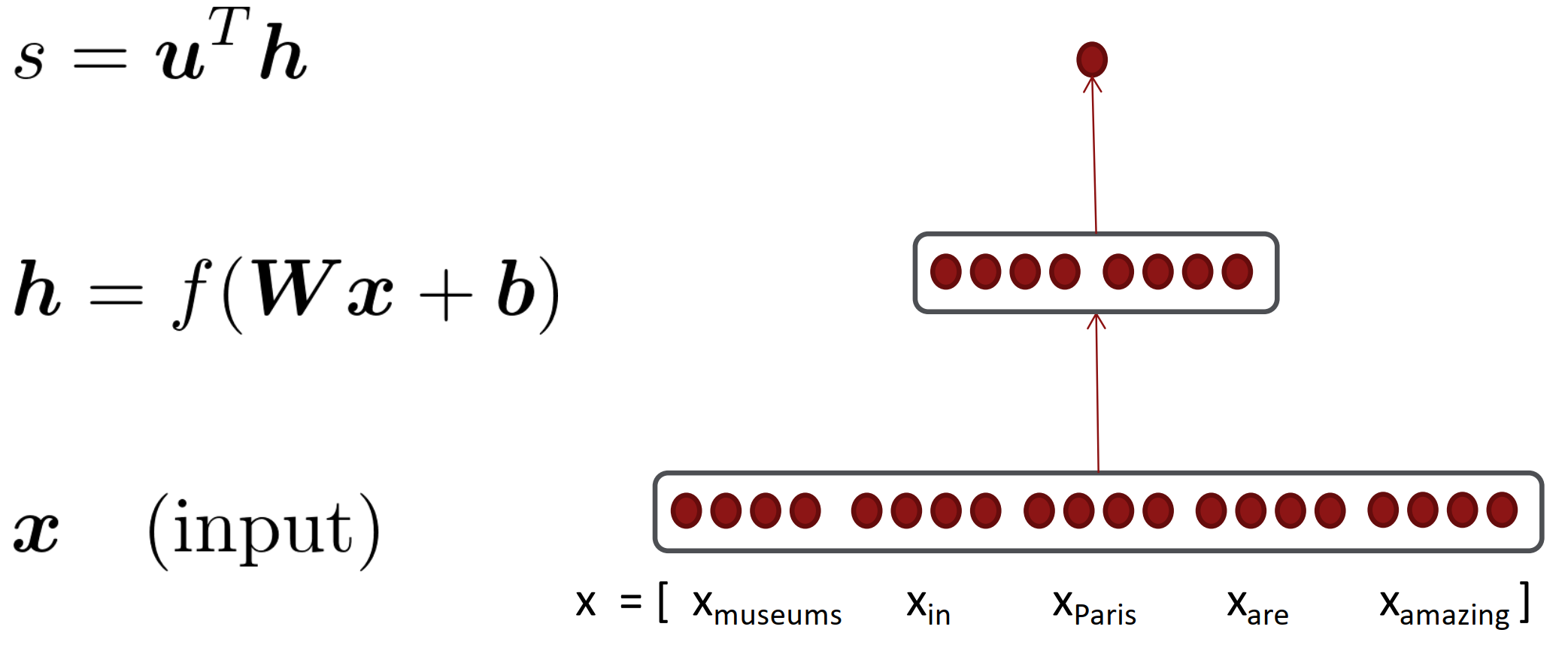
image-20210206200922955

让我们求分数s对b的梯度

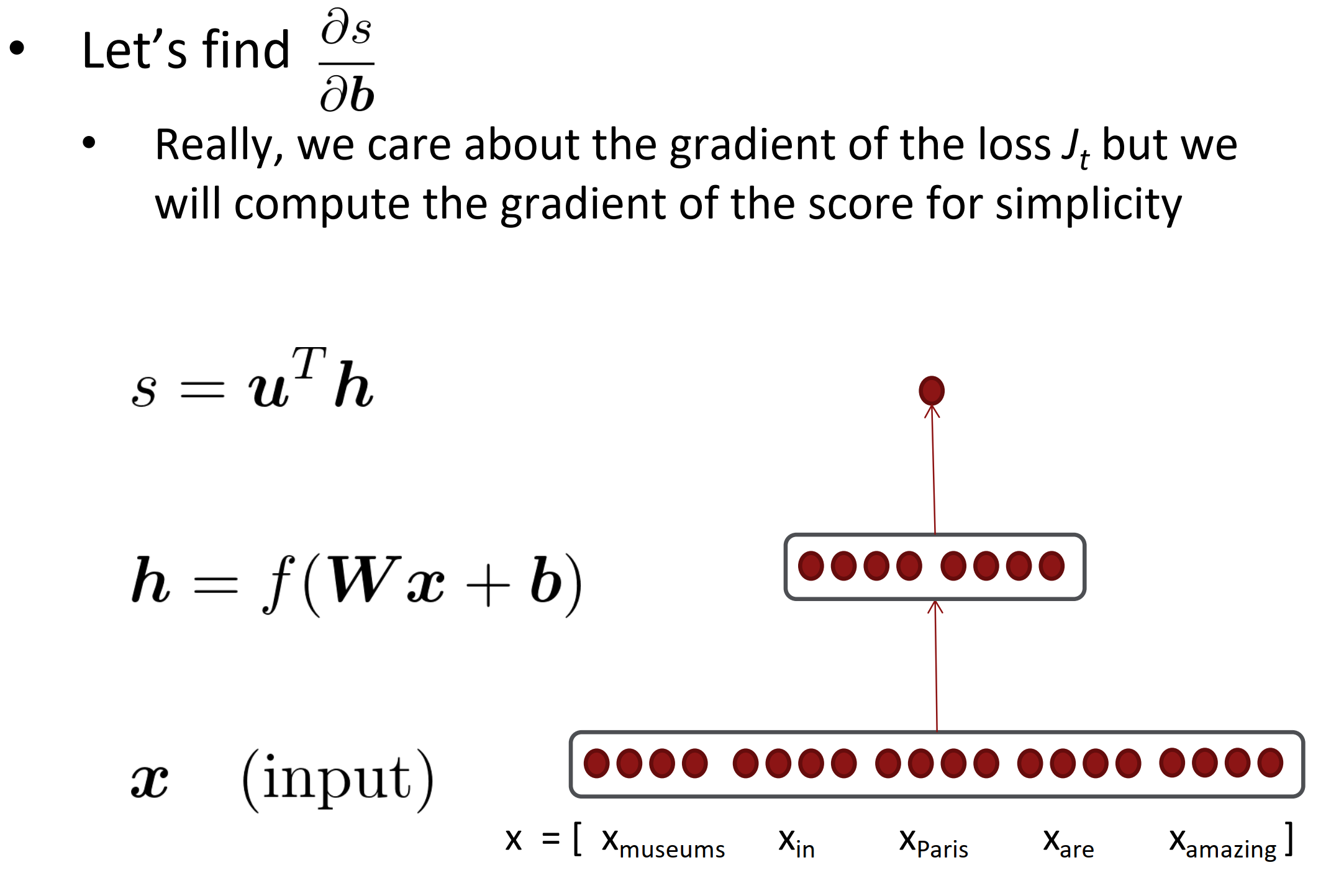
image-20210206201032566

Break up equations into simple pieces

注意，变量和保持其维度!

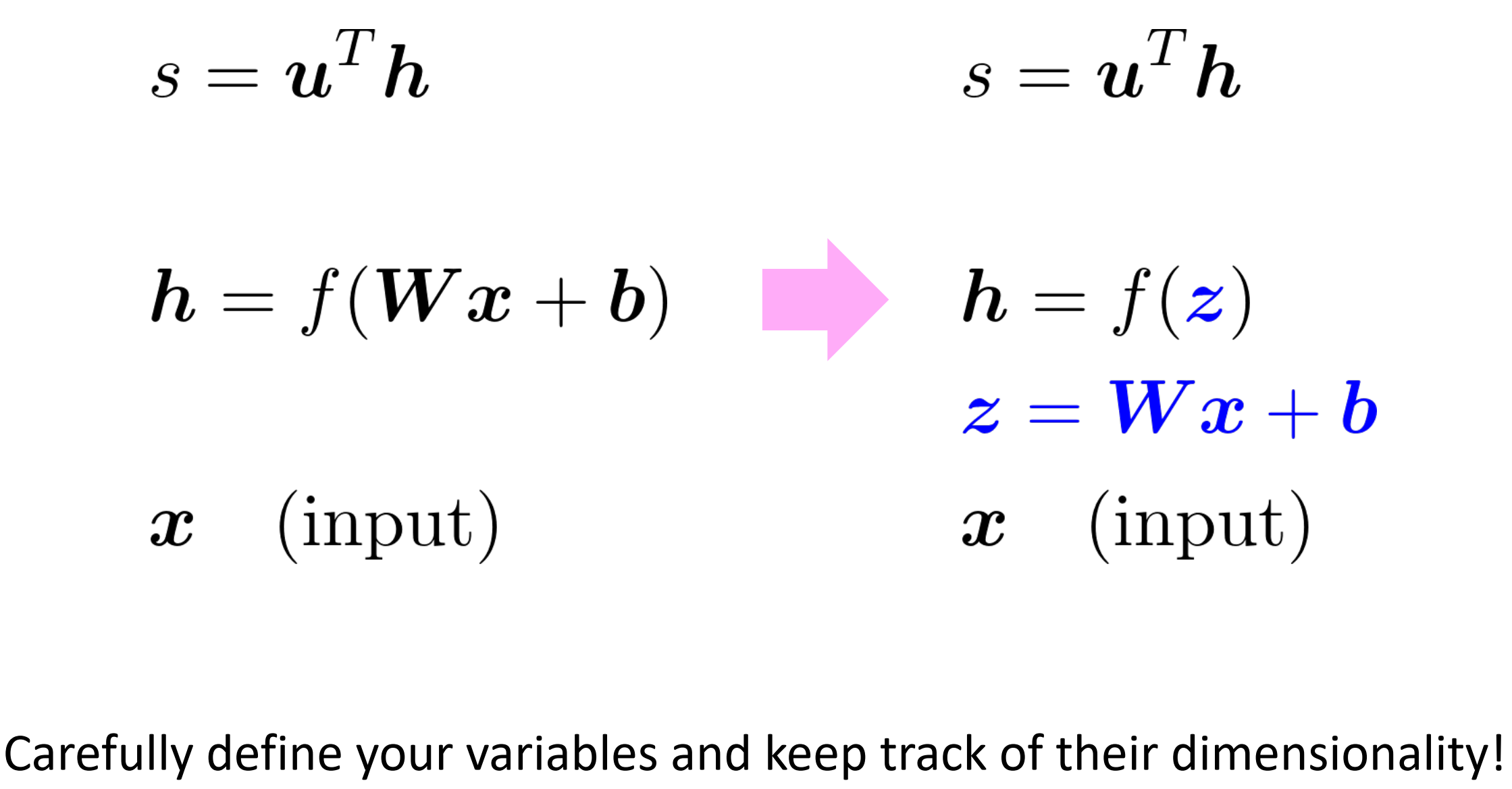
image-20210206201342047

Apply the chain rule

左边是关系式，右边是链式法则。

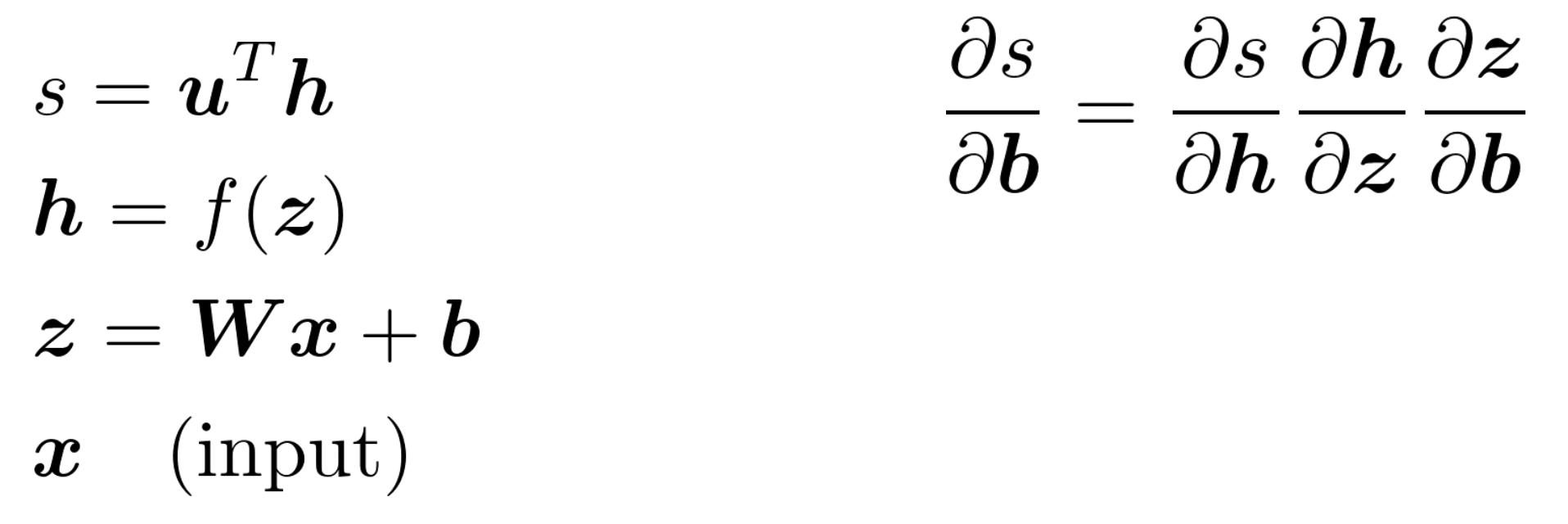
image-20210206201519446

利用方框里的公式，依次对其求导。

image-20210206201726933

Write out the Jacobians

image-20210206201912613

Re-using Computation

如果我们要求s对权重w的梯度呢？

image-20210206202128596

$\delta$是其局部误差信号，跟上面对b的梯度一样, 推出$\mathbf{u}^T \circ f^{\prime}(z)$

image-20210206202259920

关于矩阵的导数：输出形状

Derivative with respect to Matrix: Output shape , 分数s对权重的梯度形状是什么样的？

  • 1输出， nm的输入： $1 \times nm$的Jacobian。不方便接下来梯度更新
  • 让其变为$n \times m$

image-20210206202841356

矩阵的导数

分数s的梯度就等于局部误差 x 输入

image-20210206203250225

Deriving local input gradient in backprop

在反向传播中，推导局部输入的梯度。

  • 不妨只考虑单一权重$W_{ij}$
  • $W_{ij}$只影响$z_i$
  • 例如，$W_{23}$只用于祭祀$z_2$而不是$z_1$

隐层z对权重的梯度，就是每个输入。

image-20210206203526059

为什么要转置?

简单说是为了计算时维度能用，本质是因为在求外积。

image-20210206204421113

导数的形状应该是什么样的？

  • 相似地，分数对偏置b的梯度是一个行向量
    • 为了形状上的方便，称我们的梯度应该是一个列向量，因为b是一个列向量。
  • 分歧在Jacobian形式和形状方便
    • 要求作业遵循形状便利，Jacobian方便计算

image-20210206204625437

两个建议：

  1. 尽可能用Jacobian，最后reshape一下遵循形状方便
    • 在最后，分数s对偏置的偏导是一个列向量，导致$\delta$要转置
  2. 总是遵循形状方便
    • 检查维度，来弄清楚是否要转置或重组各个项
    • 错误信号$\delta$,到隐藏层要跟隐藏层维度一样

image-20210206205207422

3. 反向传播

我们几乎给你展示了反向传播。本质就是链式法则的使用。

技巧：

我们在计算低层导数时利用对高层的的求导来减少计算量。

image-20210206210236414

Computation Graphs and Backpropagation

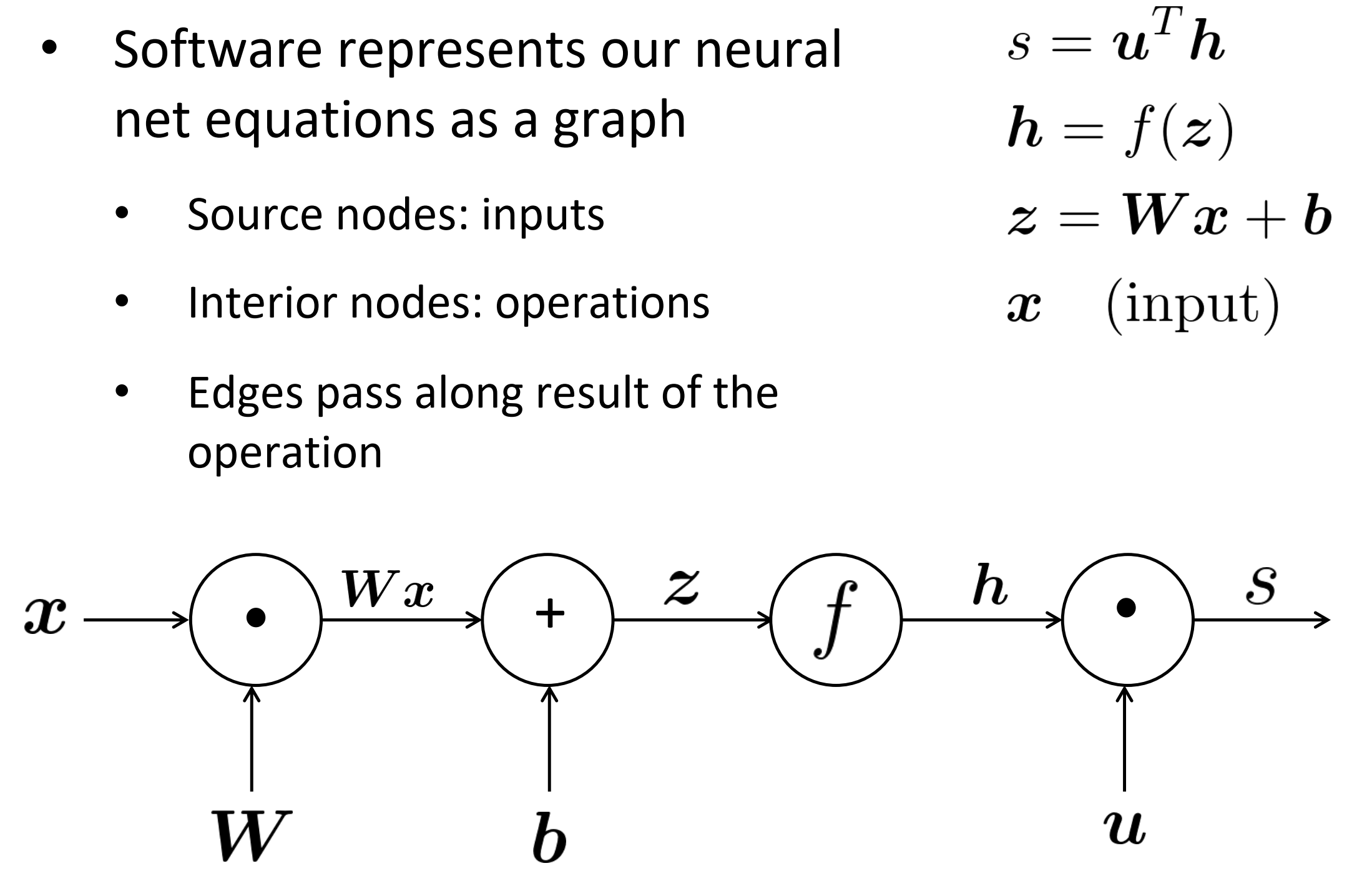
软件工程中用图来表示神经网络式子：

  • 源节点：输入
  • 内部节点：操作
  • 边传递操作的结果

image-20210206210804087

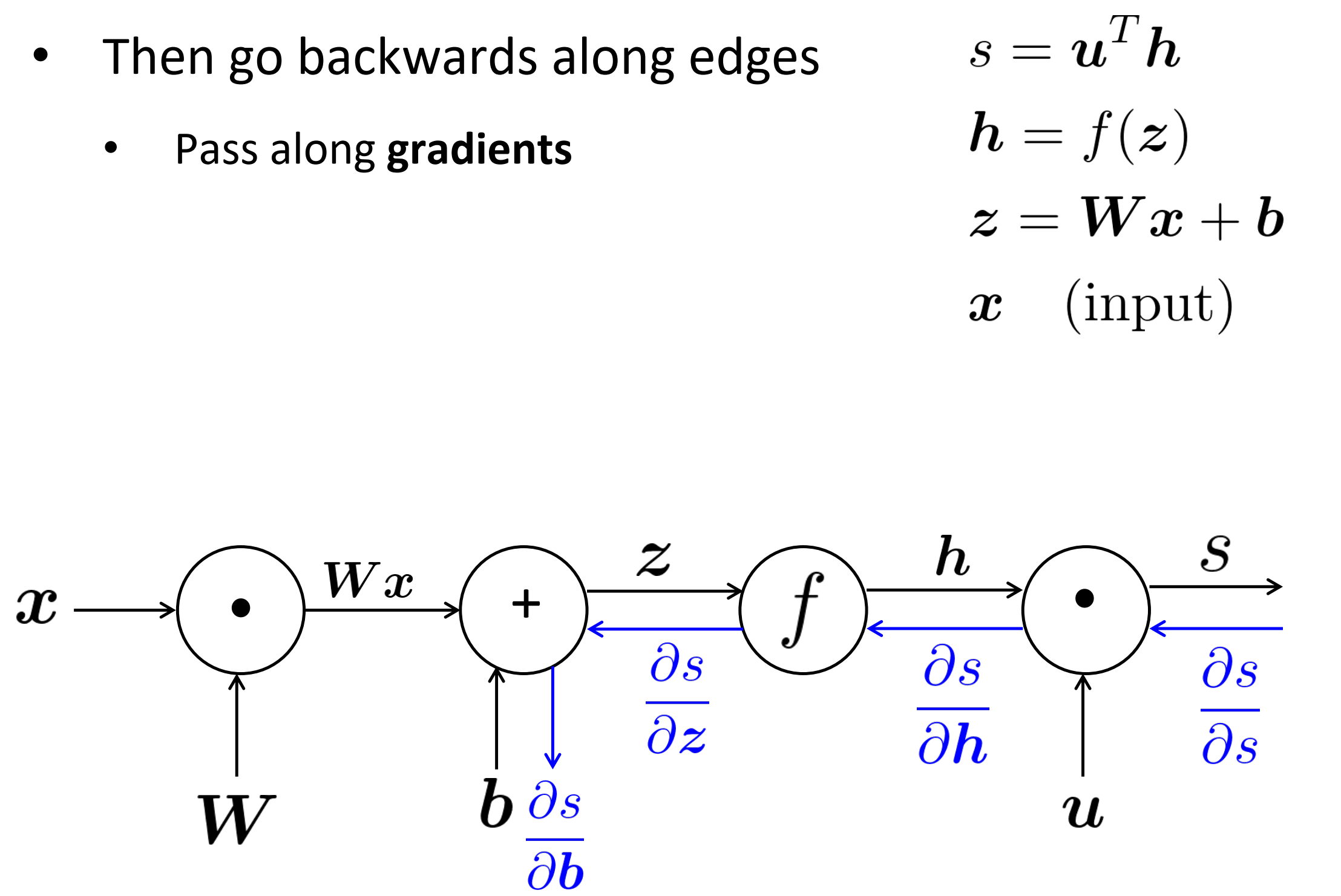
Backpropagation

在边上反向传递梯度

image-20210206211217584

单一节点的反向传播

  • 每个节点接收一个“向上流的梯度”
  • 目标是传递正确的“向下流的梯度”

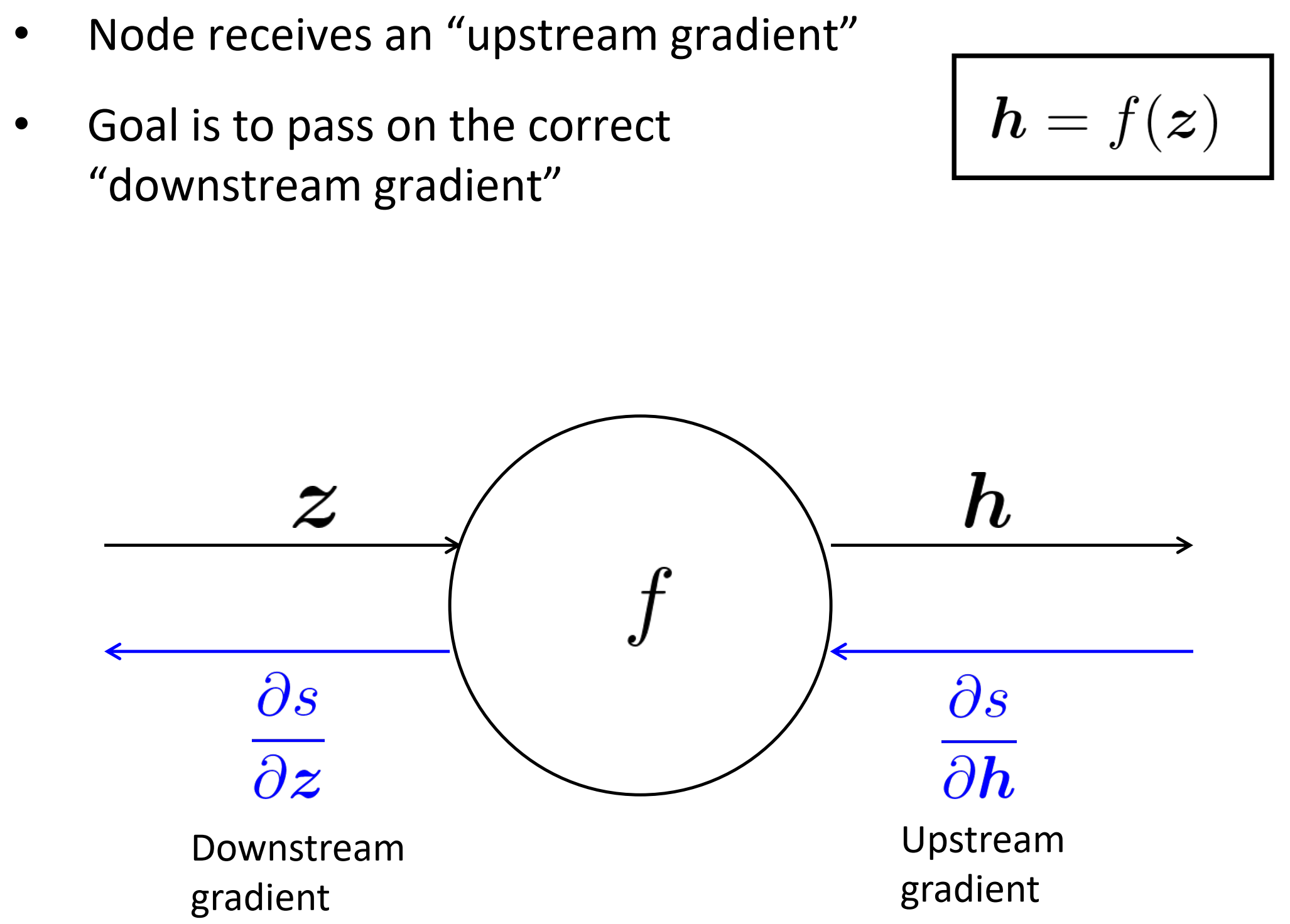
image-20210206211518562

每个节点有一个局部的梯度，这个梯度是其输出相对于其输入

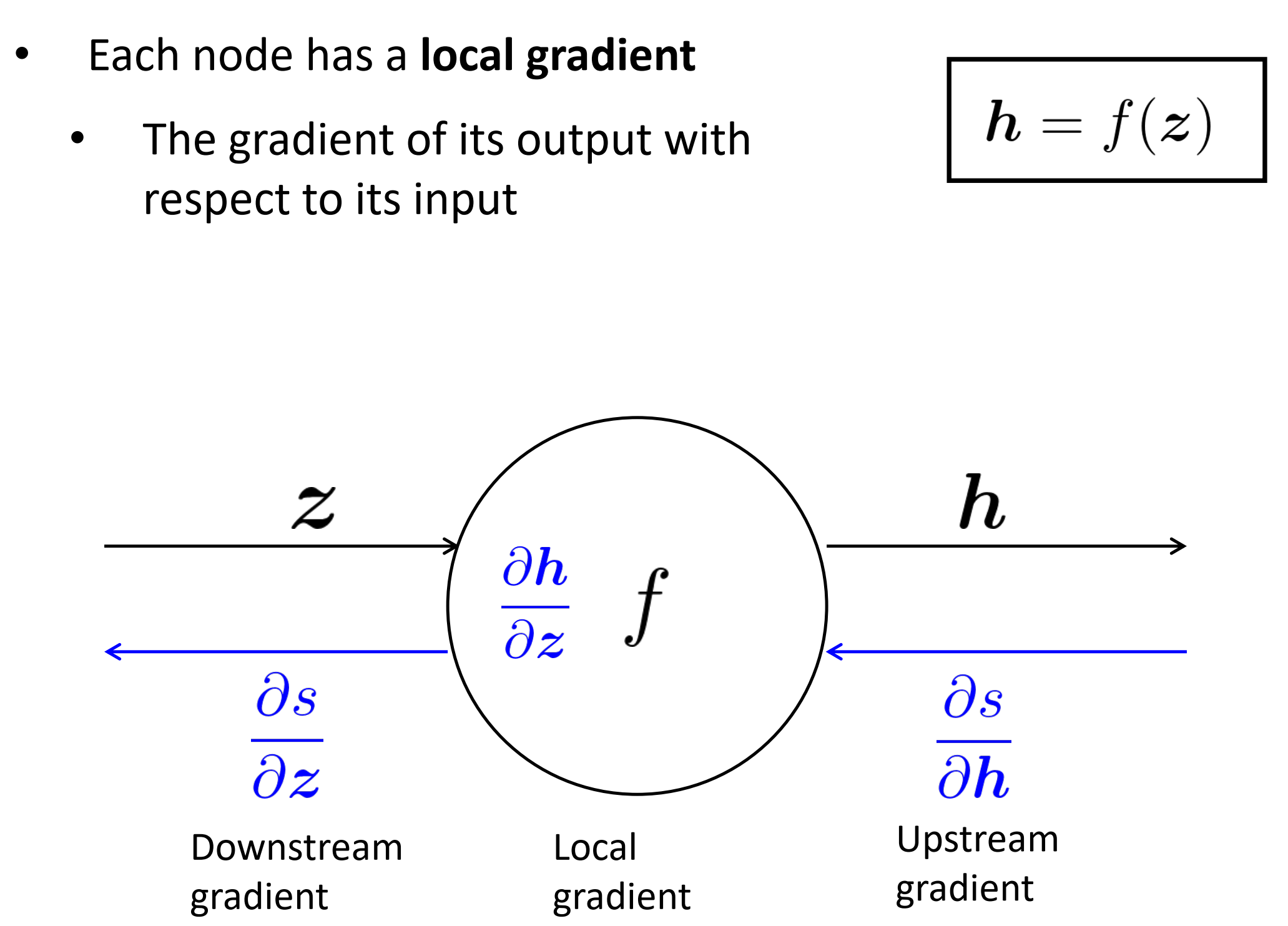
image-20210206212007268

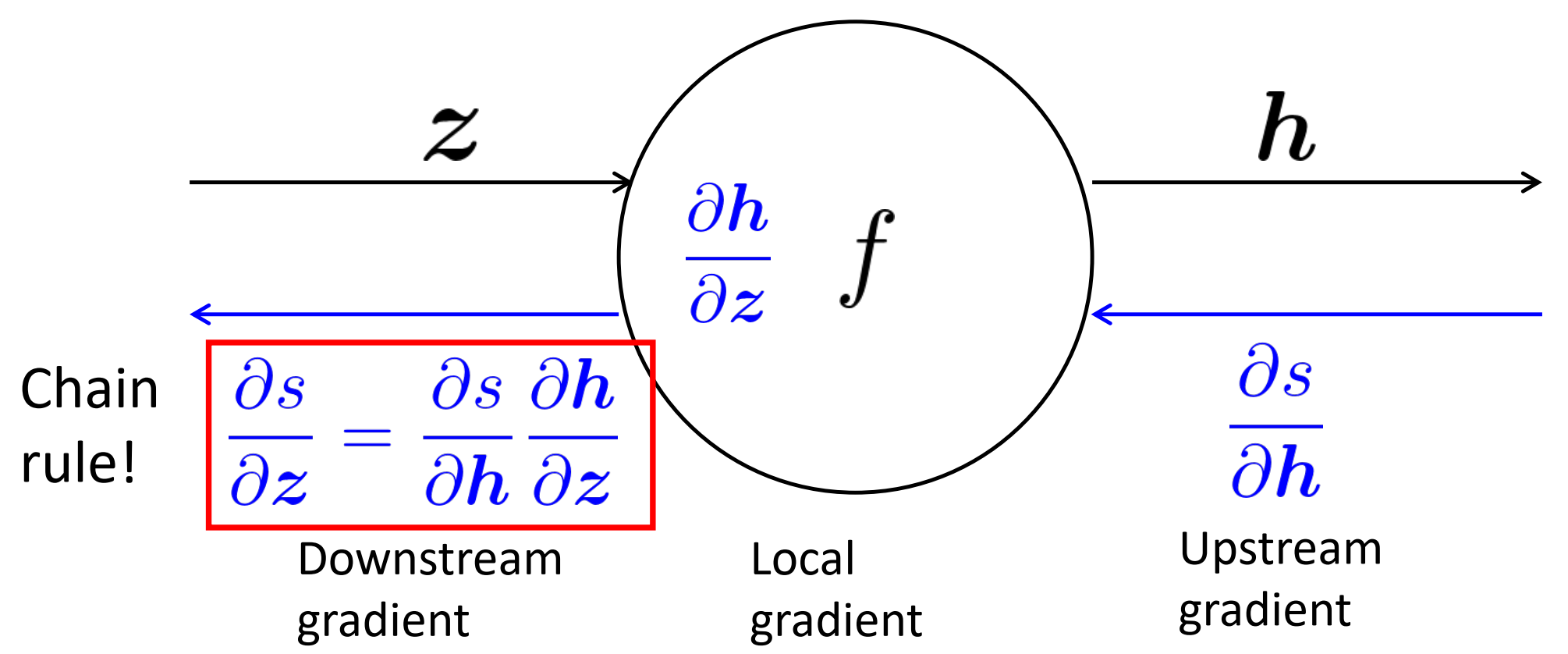
image-20210206212751321

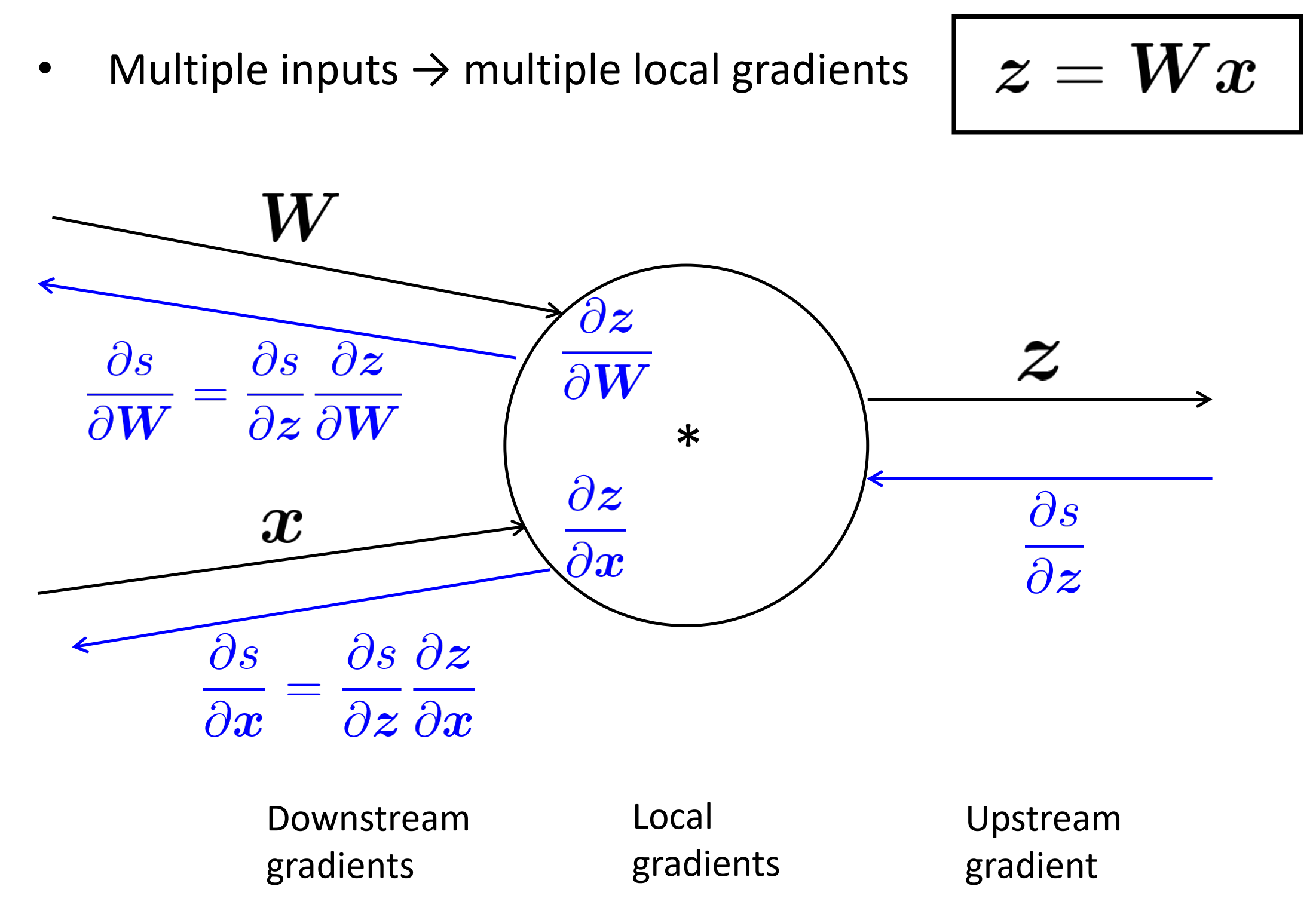
往下流的梯度 = 往上流的梯度 x 局部的梯度

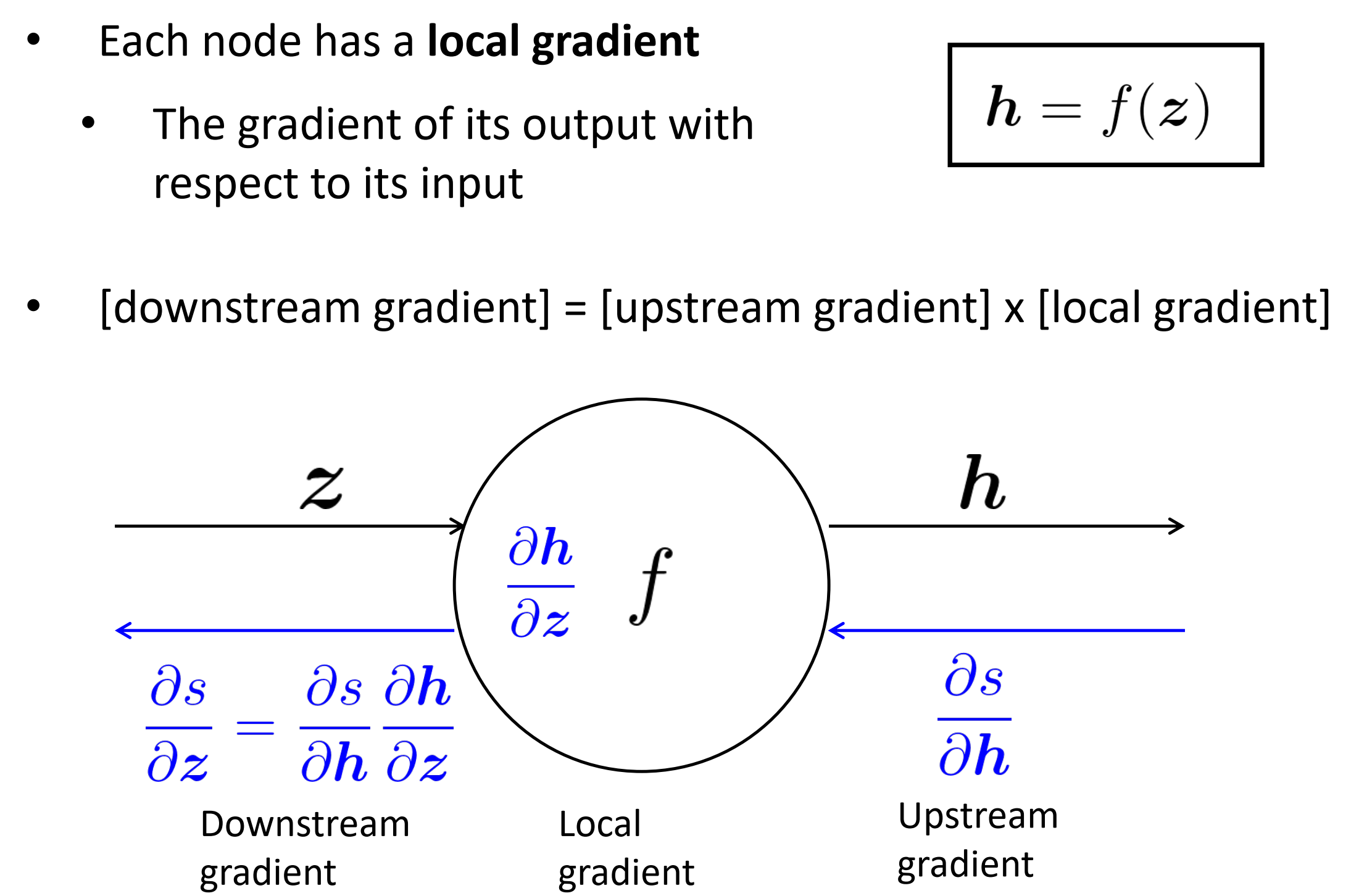
image-20210206212832132

多输入代表多个局部梯度

image-20210206212952166

例子

函数f(x)的图表示如下，每个节点输入如图。

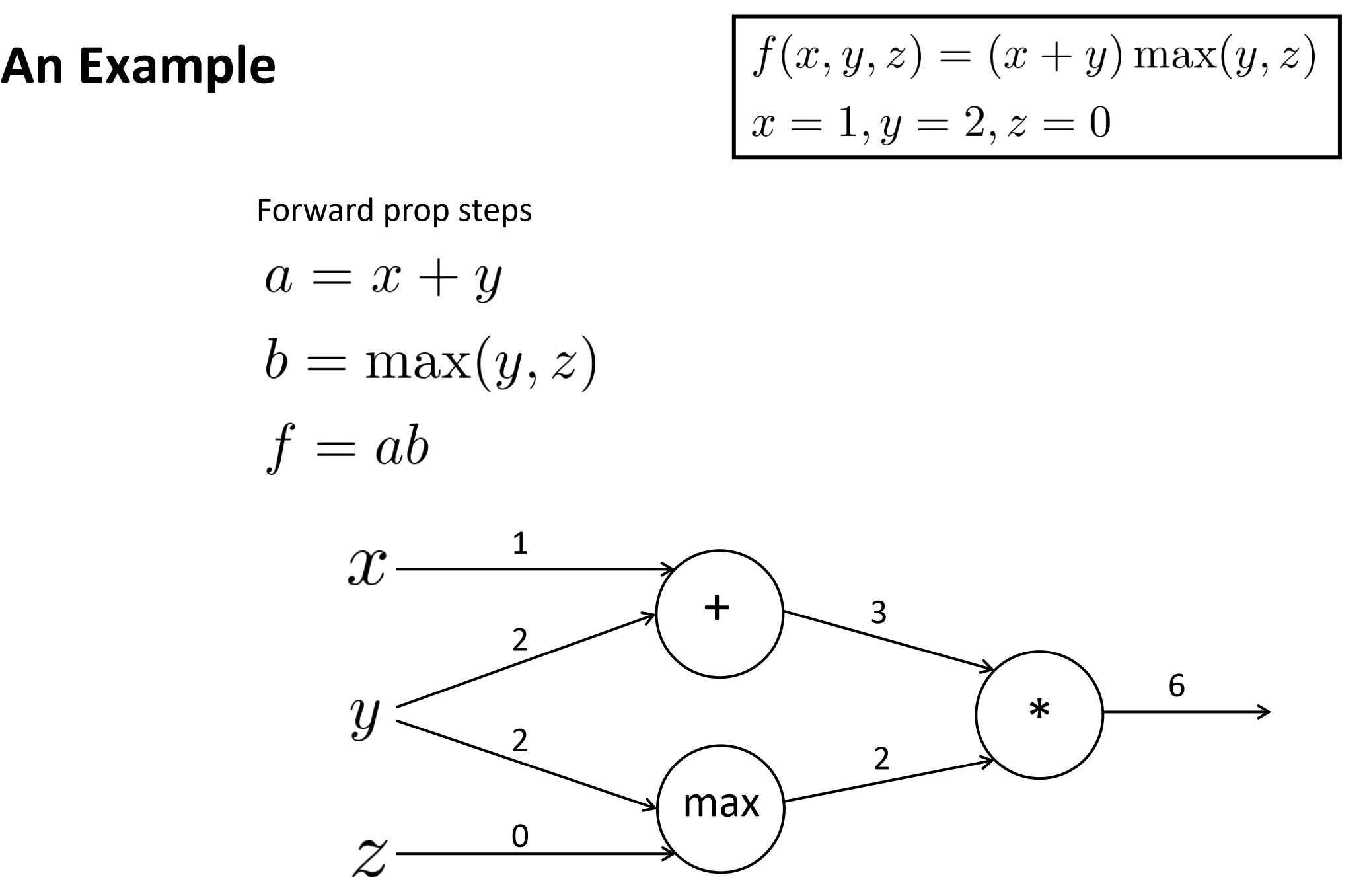
image-20210206213631261

对于第一个加节点，局部梯度: a对x， y分别为1， 1

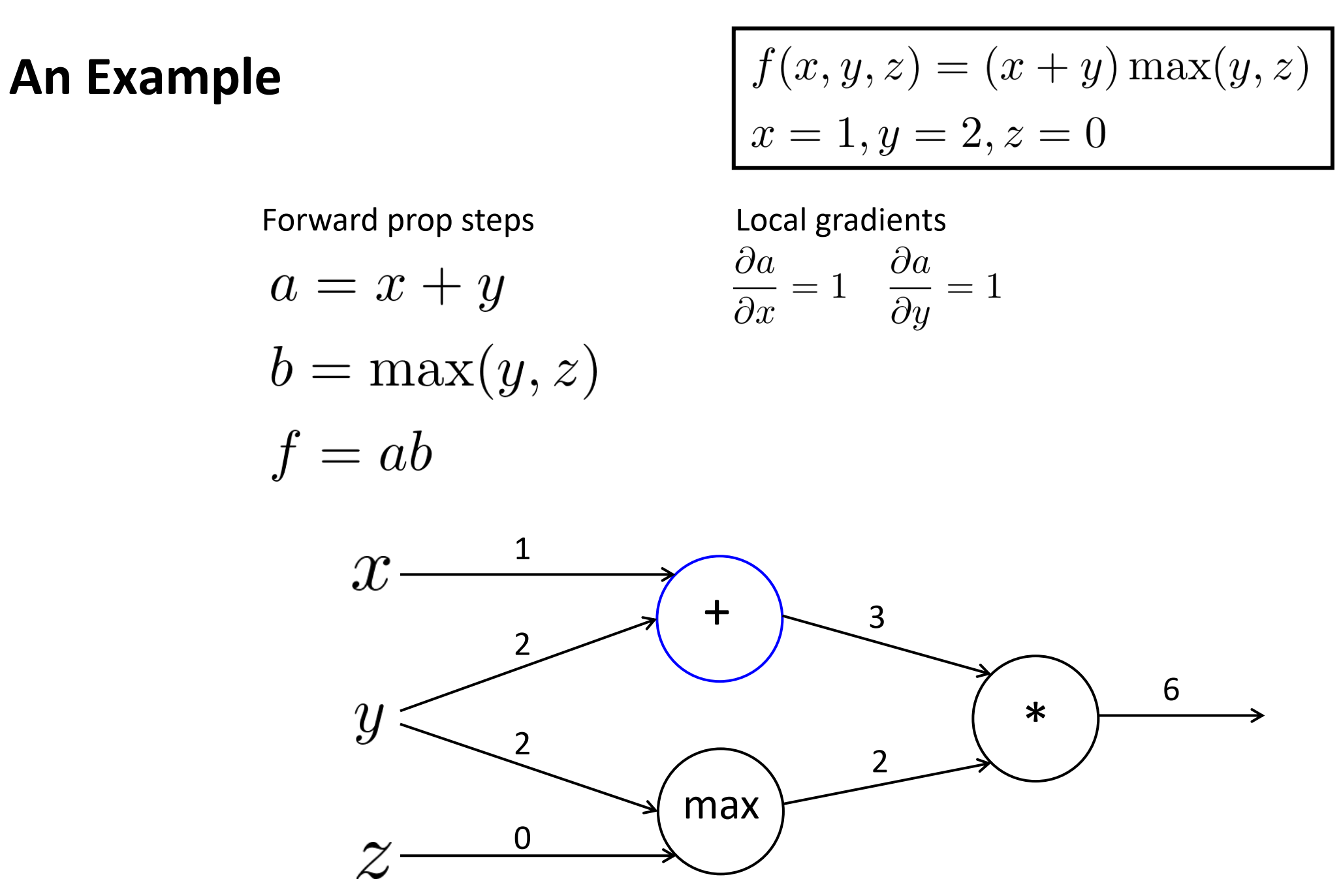
image-20210206213756796

对于 max节点， 局部梯度： b对y, z分别为1， 0

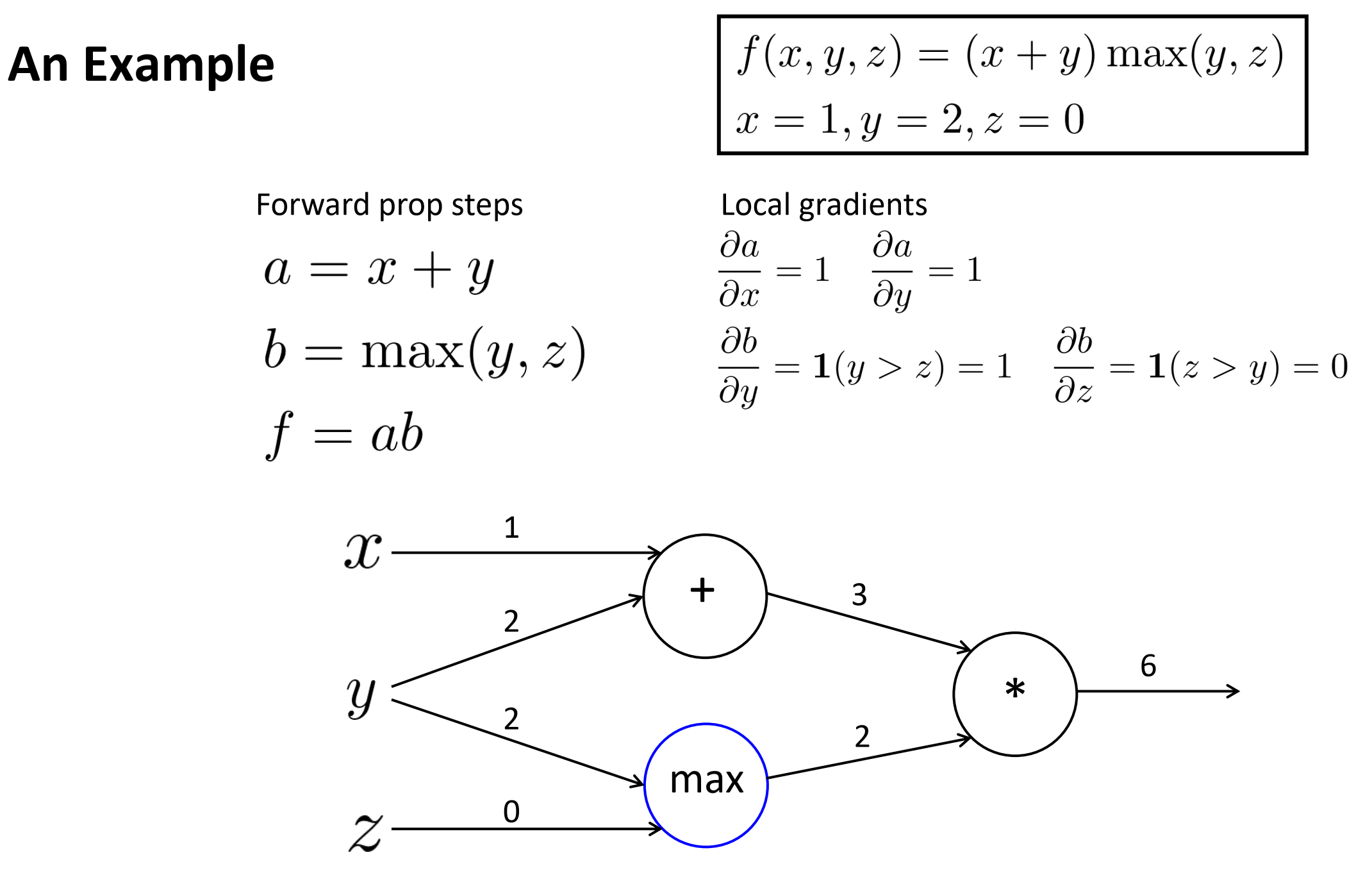
image-20210206214007847

对于 *节点， 局部梯度：f对a， b分别为2， 3

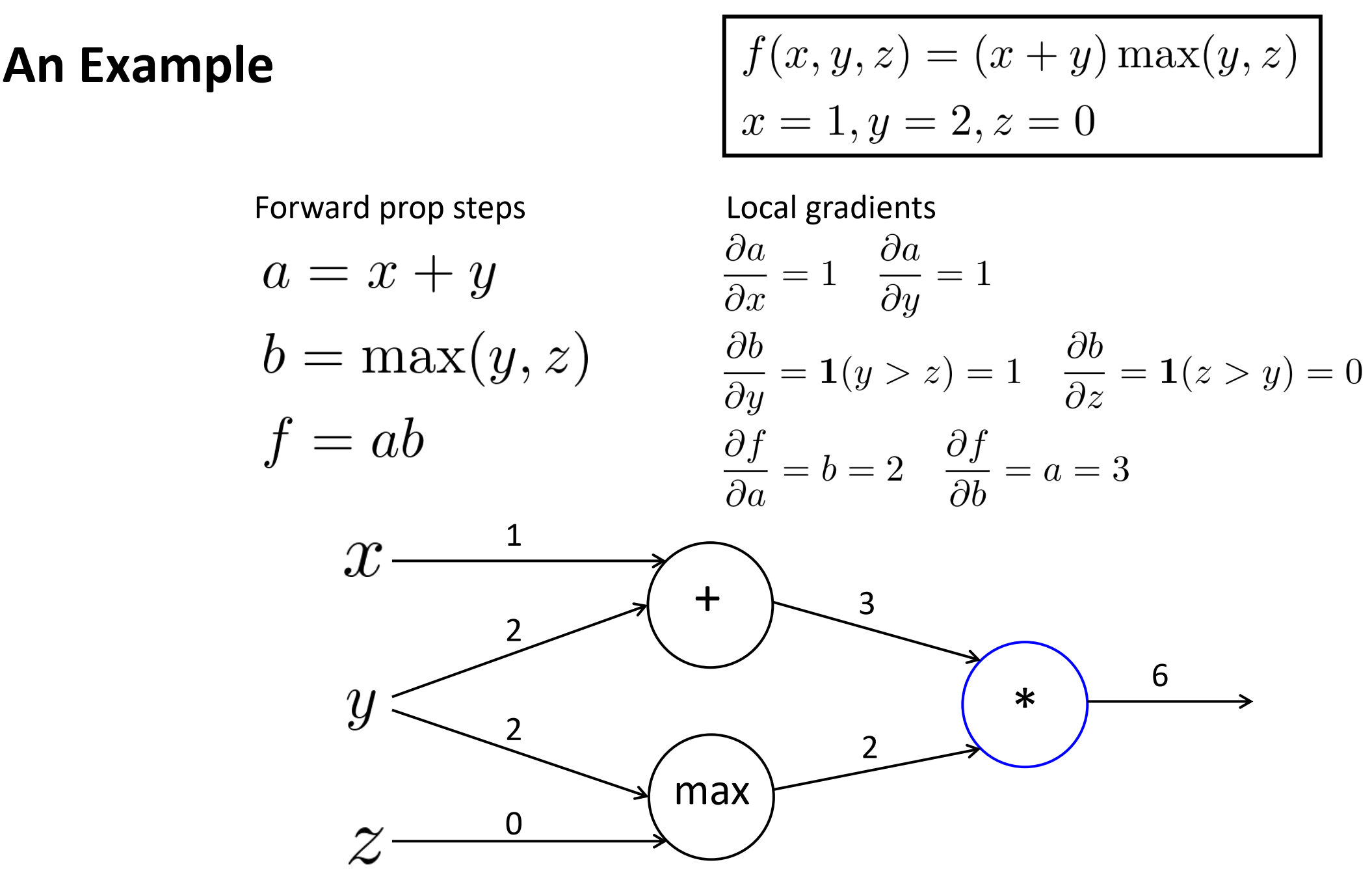
image-20210206214217247

最终反向梯度如下：

  • 局部梯度，可以理解为这个节点的梯度，算不清就让其变化0.1(比较小的值)，看对应输出变化多少，局部梯度就等于输出变化量/0.1。
    • 加法，输入边都是1
    • 乘法，互换输入
    • max，起作用的那一边是1，不起作用是0
  • 边下面就是反向传播的梯度，整个下一层的反向梯度就是节点局部梯度 x 反向传播的梯度。

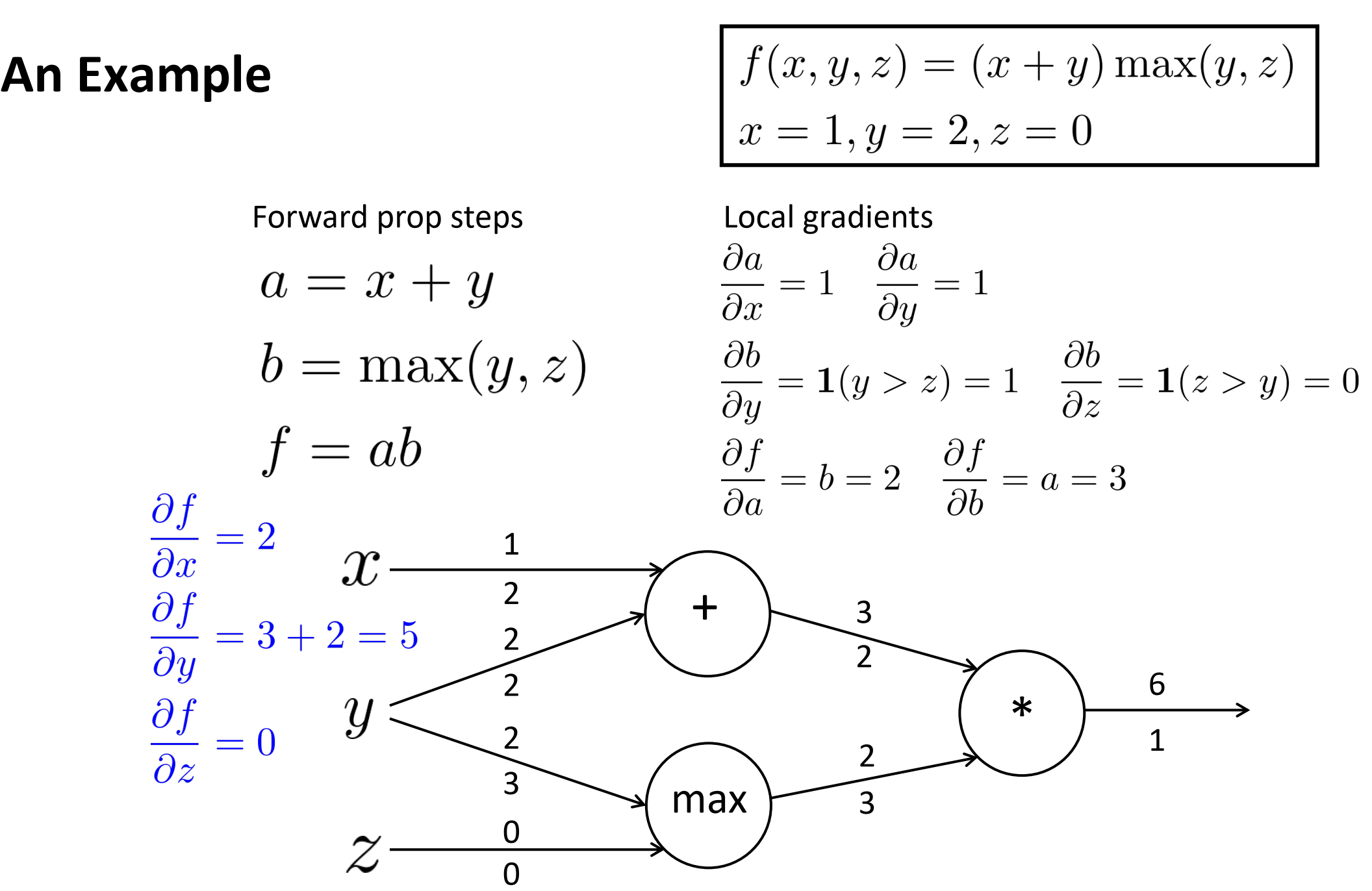
image-20210206214935426

Gradients sum at outward branches

image-20210206222325837

Efficiency: compute all gradients at once

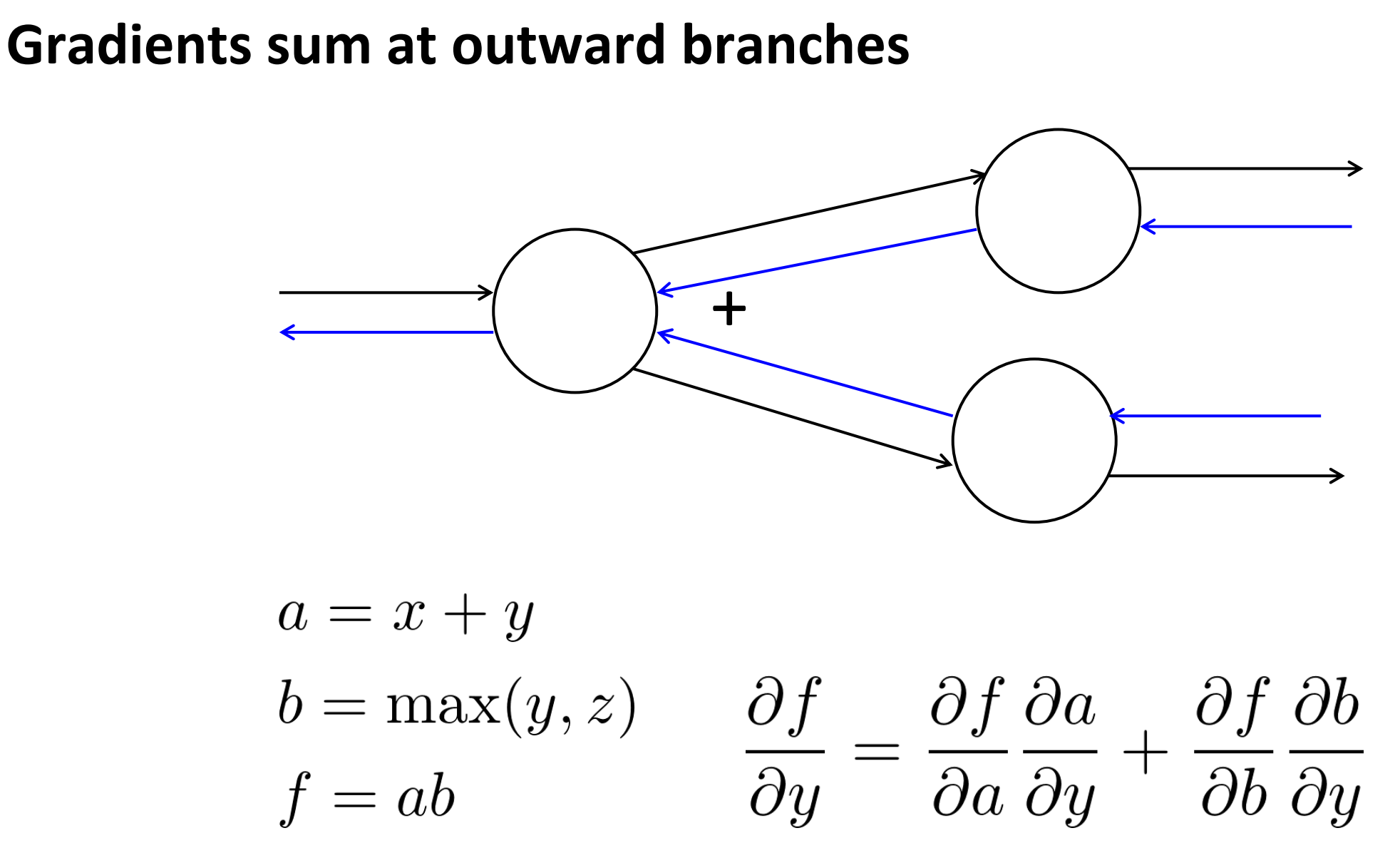
计算反向传播，不正确的方式：

  1. 一开始计算分数s对偏置b的梯度
  2. 然后独立计算，分数s对权重的梯度
  3. 这是重复计算

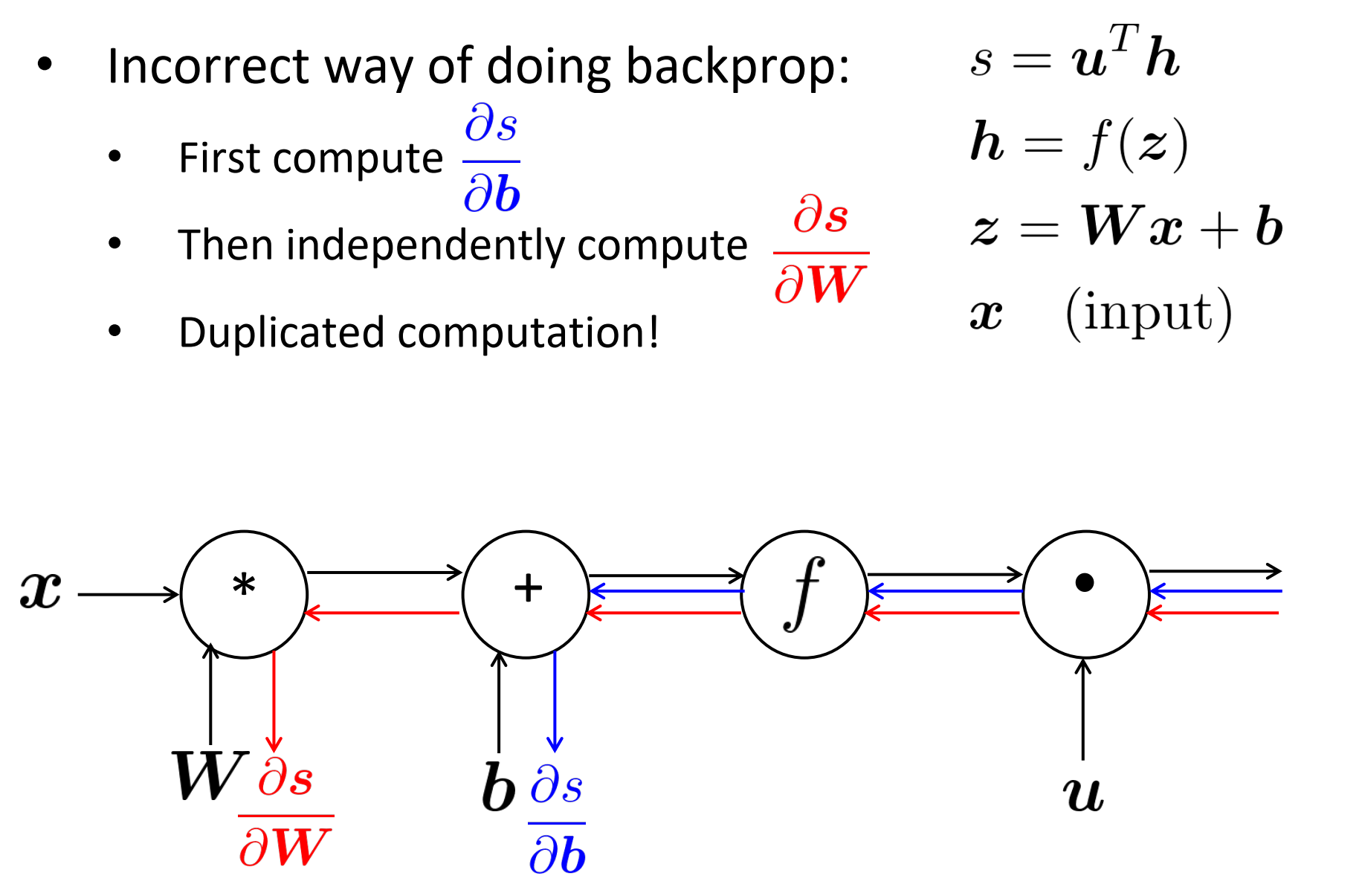
image-20210206223516711

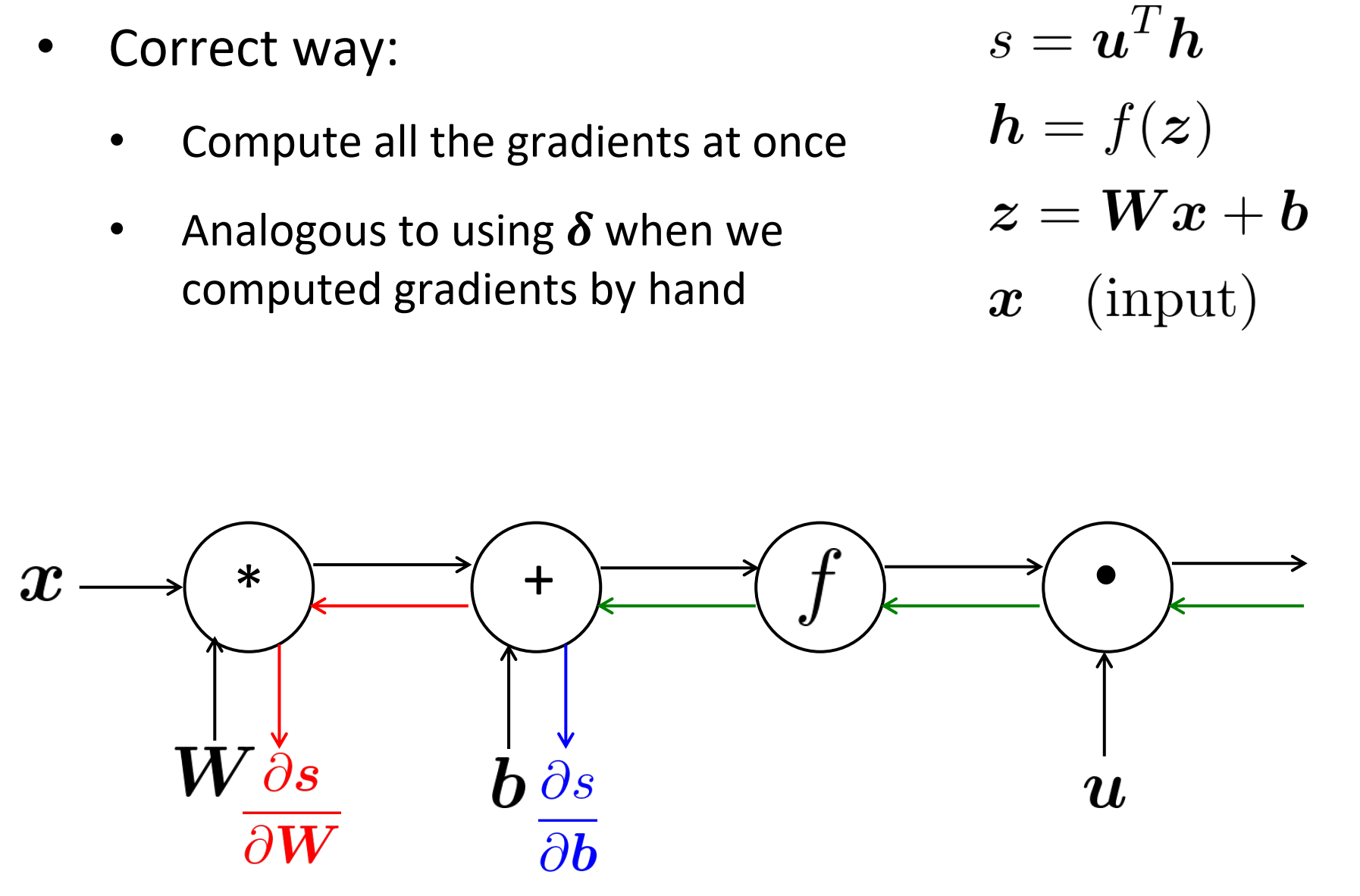
正确方式：

  • 同时计算所有梯度
  • 当手工计算梯度是，像上面类似地用$\delta$

image-20210206223651956

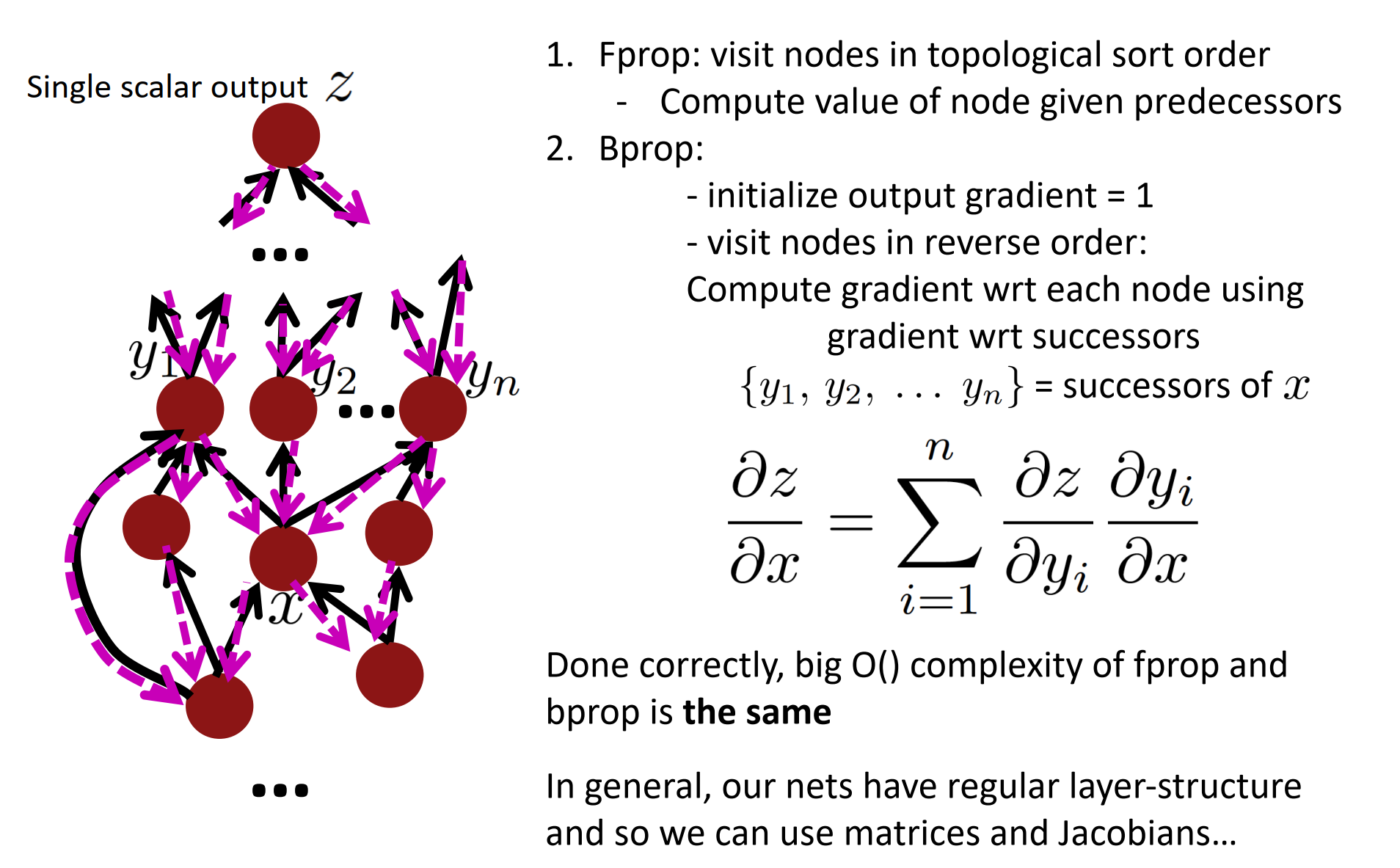
Back-Prop in General Computation Graph

  1. 前向：按拓扑排序访问节点

    • 计算给定预处理节点的值

  2. 反向

    • 初始化 输出梯度 = 1
    • 逆序访问所有节点
    • 使用节点的后继的梯度来计算每个节点的梯度

    前向和反向复杂度都是big O()，通常，我们网络是固定层结构，所以我们使用矩阵和Jacobian。

image-20210206224157886

Automatic Differentiation

自动微分：

  • 梯度计算可以从 Fprop 的符号表达式中自动推断
  • 每个节点类型需要知道如何计算其输出，以及如何在给定其输出的梯度后计算其输入的梯度
  • 现代DL框架(Tensorflow, Pytoch)反向传播，但主要是令作者手工计算层/节点的局部导数

image-20210206225146046

Backprop Implementations

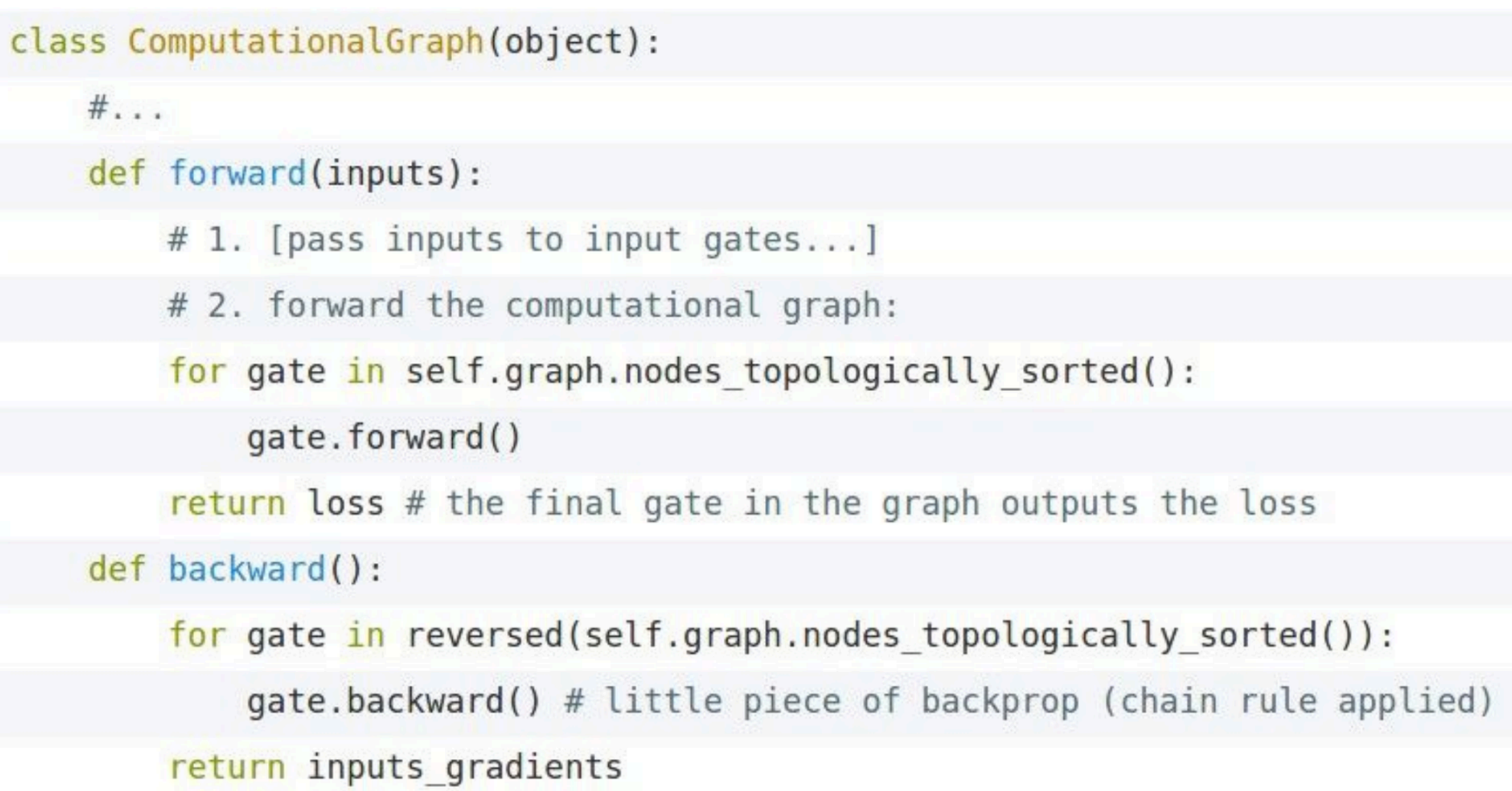
image-20210206225958824

Implementation: forward/backward API

image-20210206230040356

image-20210206230101258

Manual Gradient checking: Numeric Gradient

  • h设置为非常小的数(1e-4)
  • 容易正确实现
  • 但接近非常慢
  • 检查你的作业实现很有用

image-20210206230127732

Summary

  • 我们已经掌握了神经网络的核心技术
  • 反向传播：沿计算图递归应用链式法则
    • [downstream gradient] = [upstream gradient] x [local gradient]
  • 前向传递：计算操作结果并保存中间值
  • 反向传递：应用链式法则计算梯度

Why learn all these details about gradients?

  • 现代深度学习框架为您计算梯度
  • 但是，当编译器或系统为您实现时，为什么要学习它们呢？
    • 了解引擎下发生了什么是有用的
  • 反向传播并不总是完美地工作
    • 理解为什么对调试和改进模型至关重要
    • 参见Karpathy文章 （在教学大纲中）
  • 未来课程的例子:爆炸和消失的梯度